The vulnerability allows an attacker to extract the full ECDSA private key from BitGo Ethereum TSS wallets using a single signature and a few seconds of computation, bypassing all of BitGo security features.
Executive Summary
The Fireblocks cryptography research team found a vulnerability in the BitGo implementation of the Ethereum (ECDSA) self-managed wallet. If exploited, the vulnerability allows an attacker to steal the secret share held by the counterparty (BitGo or the client) in the TSS protocol. Attackers can bypass all security measures, gain access, and steal all the funds from the wallet.
The Zero Proof vulnerability takes advantage of missing zero-knowledge (ZK) proofs, which is the security layer of the BitGo TSS protocol. Without the ZK proofs, the protocol is reduced to a communication layer, exposing the wallet to multiple attack vectors, one of which was exploited in the Zero Proof attack outlined here.
The Zero Proof vulnerability was initially discovered in BitGoJS, the SDK that BitGo clients use to interact with the BitGo API, and which they use for performing signatures on the client side. Exploiting the vulnerability on the SDK allows an attacker to steal the private key share used by the client, regardless of their key storage methods and security measures.
On December 5, 2022, the Fireblocks cryptography research team verified the vulnerability on the BitGo REST API and backend for both testnet and mainnet accounts. This validated that BitGo was vulnerable as it was possible to extract the private key share from their proprietary HSM while bypassing both the transaction and administrative policy controls. Fireblocks immediately notified BitGo with our findings and the affected service was suspended on December 10, 2022. In February, BitGo released a patch for the vulnerability, and required its clients to update to the latest version by March 17.
Fireblocks researchers successfully demonstrated the exploits on production. The demonstration was run on bitgo.com and not on the test environment, bitgo-test.com.
Vulnerability Risk Profile
The attack extracts the private key of the Ethereum wallet, and requires very little time to execute – all it takes is a single interaction (back and forth) as part of a single signature with the other party (library or API) and a few seconds of brute-force computation to extract and expose the entire private key share.
The attack is symmetric and can be executed by both parties in the interaction or by a middleman with no prior secret material knowledge, exposing the key material to many different internal and external attackers.
The vulnerability attack surface is significantly more expansive than the exploit we showcase in this blog. This is because multiple zero-knowledge proofs are missing at later stages of the TSS protocol, creating the opportunity for more attacks.
Recommended mitigation for clients
While assets have not yet been withdrawn by attackers, it is feasible that private keys of wallets exposed to a similar class of vulnerabilities may have been compromised. As an industry best practice, Fireblocks recommends that users who created ECDSA TSS BitGo wallets prior to the fix date consider creating new wallets and transfer their funds to their new wallets.
All state-of-the-art Paillier-based protocols are immune to this attack because they contain zero-knowledge proofs of well-formedness for the Paillier modulus. This is a basic part of the protocol that is meant to make it secure against malicious key generation, which is a core premise of the protocol. It is critical to use a custody provider that builds up on well established cryptographic research.
A short introduction to Threshold Signatures and MPC
Threshold signature schemes (TSS) allow distributed parties to generate keys and multilaterally sign transactions. Applied to cryptocurrencies, threshold signatures generate shares of the private key across signing parties to eliminate a single point of failure. This means that the private key can only be compromised by exploiting enough parties with a key share. This is in contrast to traditional non-threshold signatures that only guarantee the integrity and authenticity so long as the underlying private key is not compromised.
The most popular signature scheme in the blockchain space is the Elliptic Curve Digital Signature Algorithm (ECDSA). While ECDSA is a traditional, non-threshold, signature scheme, it is possible to “thresholdize” ECDSA using Multi-Party Computation (MPC).
One of the more popular MPC protocols for threshold-ECDSA schemes is GG18 (originating from the Gennaro and Goldfeder paper), a protocol that implements homomorphic encryption and zero-knowledge proofs. At a high-level, the parties in the GG18 protocol perform calculations and exchange messages in a predetermined way. The protocol uses zero-knowledge proofs to validate that no party deviates from the protocol instructions while guaranteeing that the parties.
Technical Overview of the Attack
To explain the attack, we can use the example of a TSS protocol that is not vulnerable to this attack (Gennaro and Goldfeder), but matches well with the code in the vulnerable library on the functional level (but not on the security level).

The parts highlighted in green are implemented in the vulnerable library. This is the communication layer of the protocol. The parts highlighted in yellow and pink are not implemented at all – these are the security layers. The part in pink that was not implemented is a critical zero-knowledge proof that protects against this specific exploit (the exploit was tailored to attack the fact that this zero-knowledge proof is missing). This vulnerability was basically explained in 1998 (Gennaro, Micciancio and Rabin) and referenced in the protocol’s paper explicitly.
Simplified Explanation
Here is a summary explanation of the vulnerability that does not require understanding any of the underlying math – the equations are present to set the parameters:
- The first round of the TSS protocol requires each party to communicate a Paillier modulus (N) and V=Enc(K) using N to the other party.
- An honest actor would create N as a product of 2 big random primes.
- An attacker will instead construct this N from a combination of smaller primes and make it vulnerable to easy brute force attacks. The internal structure of the N (which is tailored to exploit the missing zk-proof) will “make it expose” the share of the other party after the attacker gets the response from the victim.
A zk-proof can’t be created for this malicious input and so the secure protocol would never be able to continue from here (thus is protected). However, to a protocol without zk-proofs – the malicious N seems as legit as any other valid N and the victim will continue the protocol by taking by the malicious V and N and performing a computation ((V^x)*Enc(beta) = Enc(K*x+beta)) on them before sending the result back.
Once the attacker gets the V^x response from the victim he will decrypt it, unpack into 16 smaller results and then perform a very simple brute force attack (16 times * 16 bits) to extract the entire secret share of the victim in a few seconds. This step is possible due to the unique nature of the malicious N and V created earlier.
The heart of the exploit
The following sections assume some familiarity with elementary modular arithmetic and group theory.
The first step in the attack is picking a faulty Paillier public key N. Under normal, honest, conditions N is the product of two random primes p and q (like an RSA modulus). The encryption process of Paillier proceeds as follows; for encrypting a value k, the sender calculates V=Enc(k)=(1+N)^k * r^N \mod N^2, where r is a random number in 1…N, called the randomizer, and sends the ciphertext V to the receiver (the technical description of the decryption process is not necessary for understanding the attack).
In the case of Paillier-based threshold ECDSA, the receiver of the ciphertexts is not the owner of the Paillier key (so it doesn’t know how to decrypt). Rather, the receiver performs a calculation on V, using its secret material, and returns the value to the original sender who actually owns the Paillier key and can decrypt the result (which is useful for calculating the final signature later).
The above works, and Paillier is a sensible encryption scheme for this purpose, because Paillier encryption admits homomorphic properties. Namely, it enables calculations over encrypted data without the need to decrypt the underlying plaintexts, thus guaranteeing privacy of the sender’s secret input. In more detail, if C=Enc(s) then V*C \mod N^2 =Enc(k+s) and V^t \mod N^2 = Enc(v*k) for any value t in 1…N, so we can add plaintexts together or multiply plaintexts by scalars by simply multiplying the ciphertexts, or taking the ciphertext to the power of the desired scalar, respectively.
So what exactly happens under the hood in the actual version of the protocol?
- The sender samples a legit Paillier key N and a random number k and sends V=Enc(k) to the receiver
- The receiver calculates C=Enc(k*x+beta)=V^x * Enc(beta) \mod N^2, where x is the secret key-shard of the receiver and beta is a random number used to mask x, and the receiver returns C to the sender.
- The sender decrypts alpha = Dec(C) which they will use at a later stage to calculate the final signature.
Notice that in an honest execution, neither C nor alpha contains information about x, so the above process does not leak any information about the receiver’s secret material if the sender does not deviate from the instructions of the protocol. Next, let’s deviate from the (uninforced) instructions of the protocol.
Sending a faulty Paillier modulus (N)
The first order of business is to create a faulty Paillier modulus. Instead of choosing N as the product of two random primes we will choose the primes p and q such that q=2p+1 (so q is a so-called strong prime with inner prime p) and we set N=p*q. We note that obtaining such a modulus randomly is virtually impossible. Next we also pick V=4 (the choice of 4 is arbitrary, we just need an arbitrary square modulo q). In the code snippet below, we further multiply the modulus N with a random big prime; this is only done to preserve the expected Paillier modulus bit length (in particular, it is not crucial for performing the attack and it does not influence the rest of the algebra).
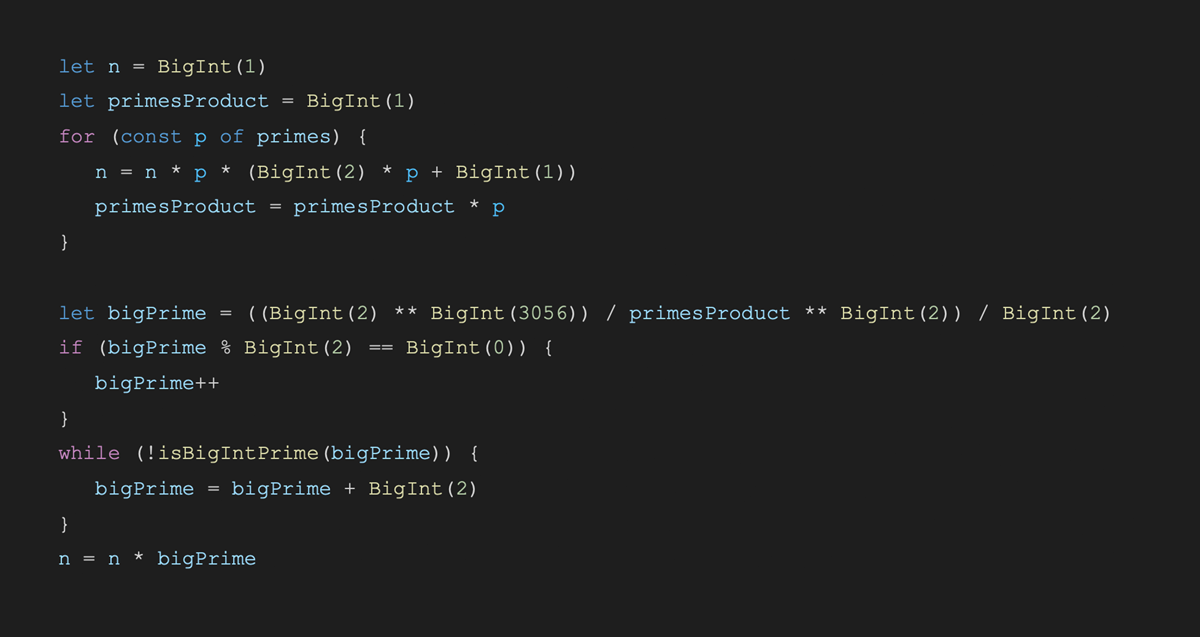

Now that we have chosen the malicious inputs, we send N and V to the receiver who replies with C=V^x * Enc(beta) \mod N^2. Next, we will show that for our choice of V and N, the ciphertext C carries a lot of information about x.
Extracting the private share from response
First, let’s reduce C modulo q:
C=V^x * Enc(beta) = V^x * (1+N)^beta * r^N = V^x r^N \mod q, where r is the randomizer chosen by the sender. Next, we calculate C^(p+1) modulo q
C^(p+1) = V^(x(p+1))* r^((p+1)pq) = V^x \mod q
The above equality holds thanks to the group structure of the units modulo q. In particular, every element of the group has order 2*p and every square in the group (including V=4) has order p. It follows that r^((p+1)pq) = 1 \mod q because (p+1)pq is a multiple of 2p, and V^(x(p+1))=V^(px)*V^x = V^x because px is a multiple of p. So, what’s next?
Notice that we have isolated the value V^x \mod q and so it is enough to calculate the (discrete) logarithm of V^x modulo q to find x (e.g. try all possible values until you land on the right one). However, this is a computationally hard problem because q and x can be pretty big numbers, so such a brute-force approach is not practical at all (d-log algorithms are not very practical either for this task). So, what now?
The trick is to make q (and p) very small, say 16 bits, and now the brute-force attack is very easy, although it would only yield the value of x modulo p, rather than the entire x (because the modular reduction occurs in the exponent implicitly). To get the rest of the bits, we simply choose many such primes and repeat the attack. Namely, we set N = p1q1*p2q2*…*p16q16 (where each q hides the associated p as an inner prime), and we repeat the aforementioned process for each prime to obtain:
x1 = x \mod p1
x2 = x \mod p2
…
…
x16 = x \mod p16
Using the 16 xi’s above, we can reconstruct the shard x uniquely using the famed Chinese Remainder Theorem.
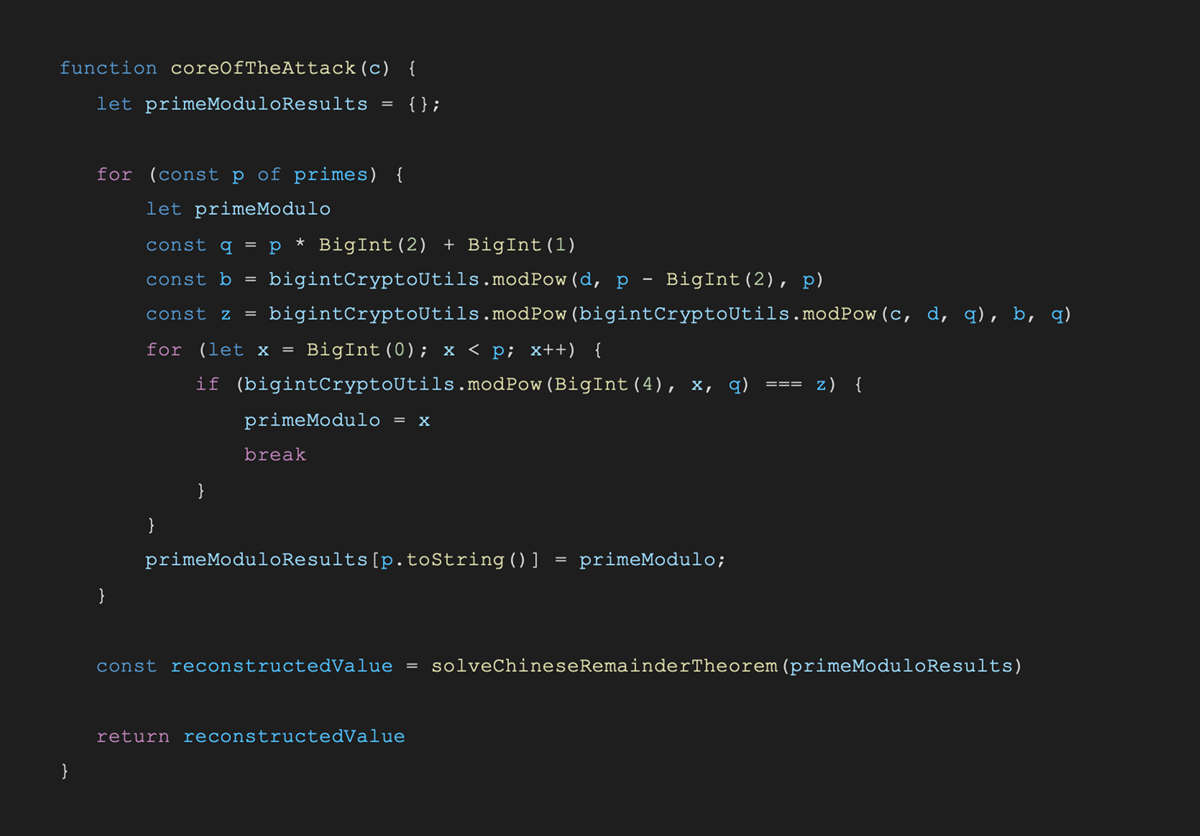
This code of the vulnerable ECDSA library is located at ecdsa.ts.
Coordinated Disclosure with BitGo
This publication is released at the end of a “coordinated disclosure” process that the Fireblocks’ research team has followed with BitGo’s security team. Upon verification that the Zero Proof vulnerability is actually exploitable in a real world scenario, Fireblocks immediately reached out to the BitGo security team and notified them of the vulnerability, attached a detailed technical report with a working POC that exploits the vulnerability, and made it clear that client funds are at risk.
Timeline
December 5, 11:08 AM EST – Fireblocks validated the vulnerability both on testnet and mainnet.
December 5, 3:11 PM EST – Fireblocks notified BitGo of the vulnerability.
December 5, 7:12 PM EST – BitGo security team confirmed receipt and promised to deliver a timeline for remediation.
December 8 – After 3 days without any communication, Fireblocks noticed that BitGo had removed the option to create new Ethereum wallets ( in some accounts) but existing wallets were still active and vulnerable.
December 9, 3:55 PM EST – We received an email from BitGo claiming the vulnerability was only relevant on developer testnet accounts. This comes multiple days after we already extracted a private key on mainnet, against the BitGo API as well as on the JS library. Contrary to the communication we received, BitGo launched the TSS wallets into general availability in October 2022 through a tweet and a blog post.

December 10, 3:15 AM EST – To validate our claim, we ran the POC again on BitGo’s API on mainnet and extracted the secret share again – we found that the vulnerability had still not been remediated despite the claim it was never live in production.
December 10, 1:58 PM EST – We finally received an error on the mainnet account that withdrawals on TSS wallets are disabled, both on UI and API.
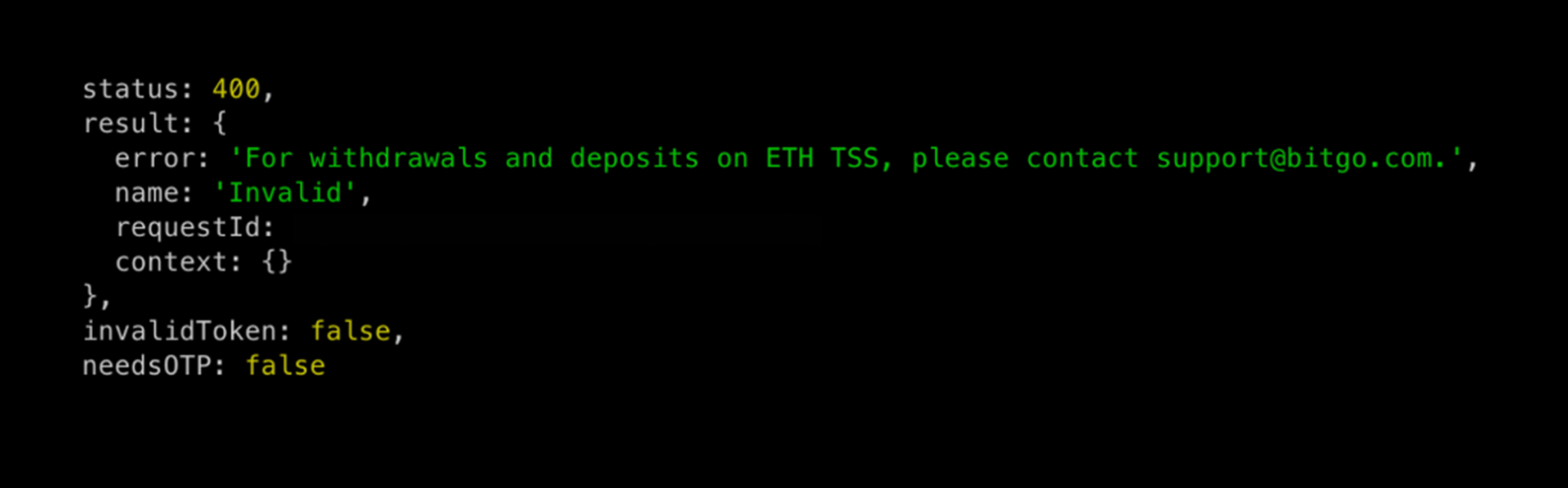

December 16, 7:37 PM – Bitgo confirmed the remediation and Fireblocks considers the vulnerability to be mitigated for any new attacker(s).
All analysis of the vulnerability, risk, exposure and attack scenarios are based on the Mathematical proof, POCs we ran successfully, and the understanding of inner workings of all relevant systems to the best of our ability. We believe that the Fireblocks cryptography research team’s work described in this report helped ensure the security of a significant amount of customer funds.



